Integrale indefinito – definizione + esercizi
L’integrale indefinito è un concetto centrale nel calcolo integrale. In matematica, rappresenta l’insieme di tutte le primitive di una funzione, ovvero tutte le funzioni la cui derivata è uguale alla funzione data.
Definizione integrale indefinito
La definizione dell’integrale indefinito è la seguente:
Se F′(x) = f(x), allora
∫f(x)dx = F(x) + C,
dove C è una costante reale arbitraria, chiamata costante di integrazione.
L’integrale indefinito permette di risalire alla funzione originaria a partire dalla sua derivata. Si tratta di uno strumento essenziale in matematica e viene utilizzato anche in fisica, ingegneria e altre scienze applicate.
Esercizi – Calcolo di integrali indefiniti
Calcola l’integrale indefinito della funzione:
(usa le formule base per le funzioni elementari)

Calcola l’integrale indefinito della funzione:
(usa un opportuno cambiamento di variabile)

Calcola l’integrale indefinito della funzione:
(usa il metodo di integrazione per parti)

Calcola l’integrale indefinito della funzione:
(usa la scomposizione in fratti semplici)
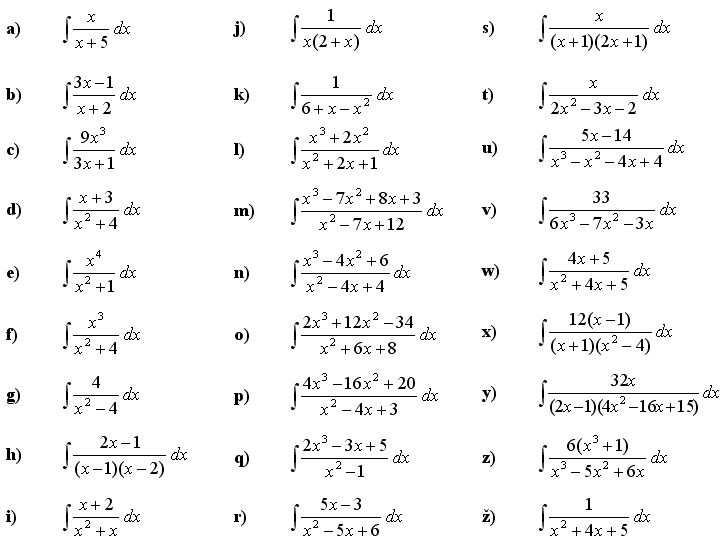
Calcola l’integrale indefinito della funzione:
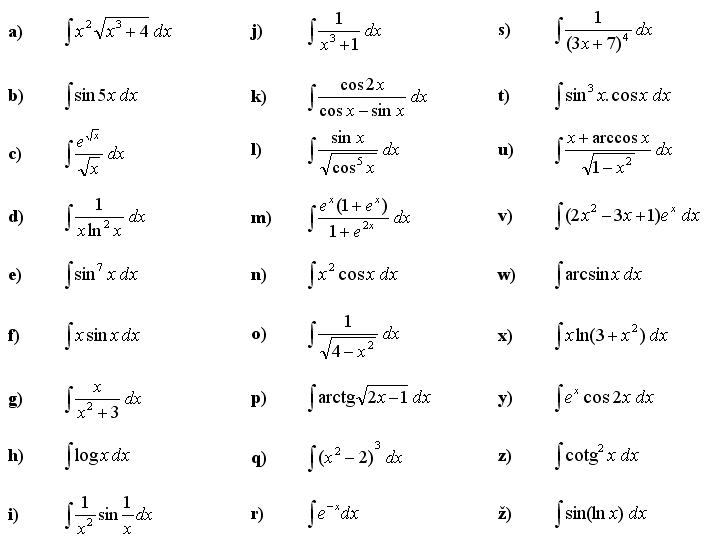
Calcola l’integrale indefinito della funzione:
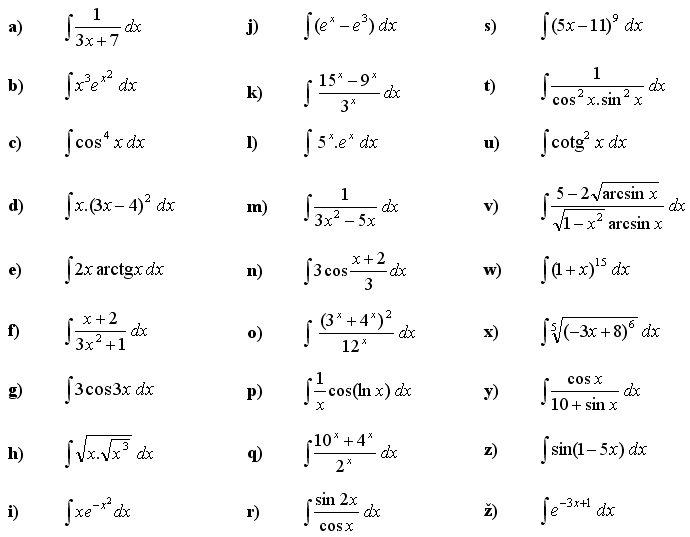
Calcola l’integrale indefinito della funzione:
